This week in advanced statistics, we covered hypothesis testing and correlation analysis. We were assigned three questions to answer, which read as follows: 

The director of manufacturing at a cookie factory needs to determine whether a new machine is producing a particular type of cookie according to the manufacturer’s specifications, which indicate that cookies should have a mean of 70 and standard deviation of 3.5 pounds. A sample of 49 cookies reveals a sample mean breaking strength of 69.1 pounds.

For question A, the null hypothesis is μ = 70 and the alternative hypothesis is μ ≠ 70. To determine whether or not the machine is meeting the manufacturer’s specifications for average strength, I will be conducting a two-tailed test. There is not significant evidence to reject H0. The p-value of this is 0.07186, which is not significant as p is not less than the significance level of 0.05, which means the sample meets manufacturing standards. Redoing part B with a standard deviation of 1.75 causes us to reject H0, as the p value produced is less than the significance level 0.05. Redoing part B with a sample mean of 69 pounds and a standard deviation of 3.5 pounds produces a z score of -2 and a p value of 0.0456, causing H0 to be rejected. Second Question:If x̅ = 85, σ = standard deviation = 8, and n=64, set up 95% confidence interval estimate of the population mean μ.

The confidence interval estimate of the population mean would be (83.04, 86.96). The accompanying data are: x= girls and y =boys. (goals, time spend on assignment)  
a. Calculate the correlation coefficient for this data set _____
b. Pearson correlation coefficient _____
c. Create plot of the correlation

For this question, I used the following R code: 

library(“lsr”)

library(“corrgram”)

x <- data.frame( cbind(Goals = c(4,5,6),

  #Grades = c(“49″,”50″,”69”),

 # Popular = c(“24”, “36”, “38”),

  Time_on_assignment = c(92, 108, 135)

  #Total = c(“92″,”108″,”135”)

)

)

y <- data.frame(cbind(Goals = c(4,5,6),

  #Grades = c(“46.1″,”54.2″,”67.7”),

  #Popular = c(“26.9”, “31.6”, “39.5”),

  Time_on_assignment = c(18.9, 22.2, 27.8))

  #Total = c(“95.9”, “113”, “141”))

)

girl_goals <- as.matrix(x$Goals)

boy_goals <- as.matrix(y$Goals)

girl_time <- as.matrix(x$Time_on_assignment)

boy_time <- as.matrix(y$Time_on_assignment)

cor(x = girl_goals, y = boy_goals)

cor(x = girl_time, y = boy_time)

cor(x = girl_goals, y = boy_goals, method = “pearson”)

cor(x = girl_time, y = boy_time, method = “pearson”) 

cor(x = girl_goals, y = boy_goals, method = “spearman”)

cor(x = girl_time, y = boy_time, method = “spearman”) 

goals <- data.frame(girl_goals, boy_goals)

plot(girl_goals, boy_goals)

plot(girl_time, boy_time)

These are the produced plots: 

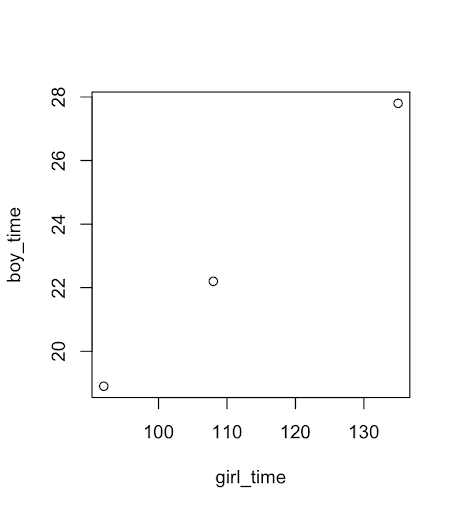
The Pearson correlation coefficient for goals is 1 and time is 0.9999989, and the Spearman correlation coefficient for both goals and time is 1.